荒川、掘っちゃいましょう
荒川どう掘るの?
の続きです。
岩淵水門
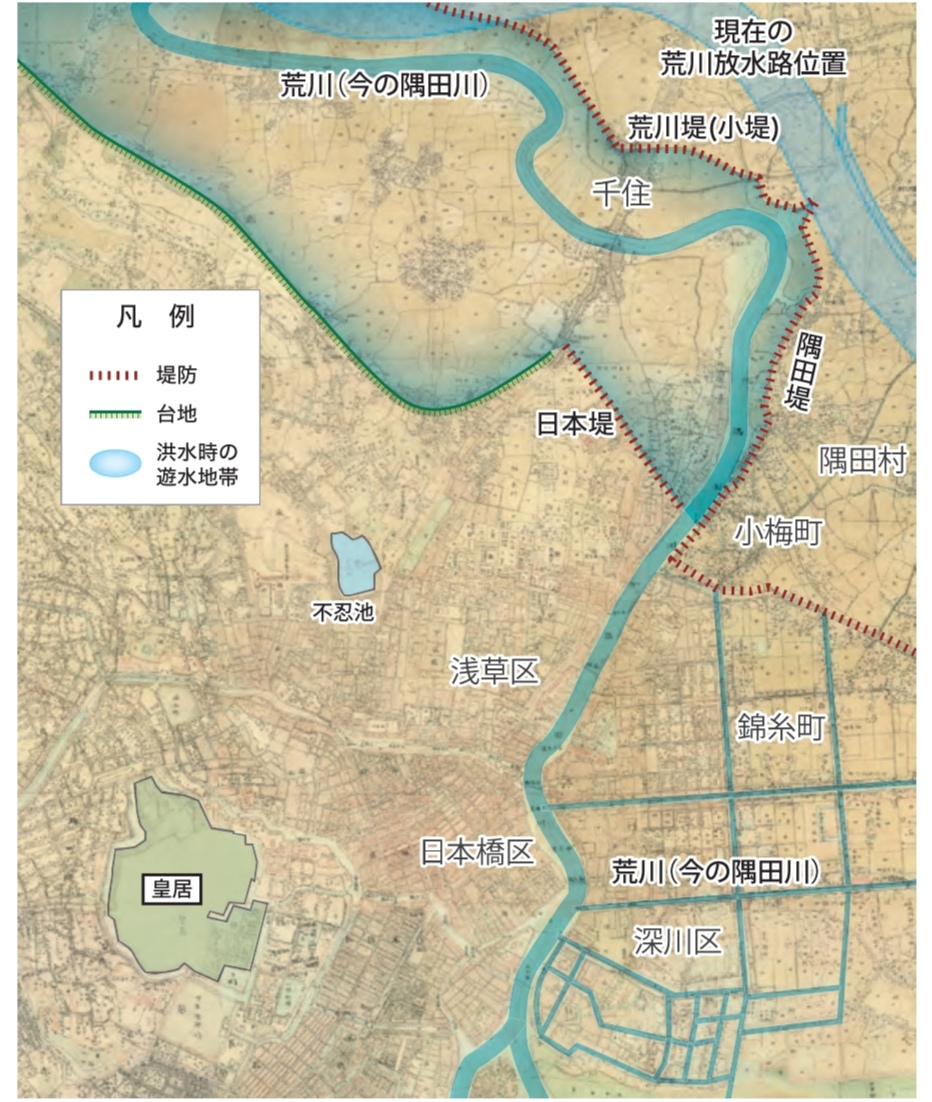
それまで、荒川は下流を隅田川と呼んでいたけど
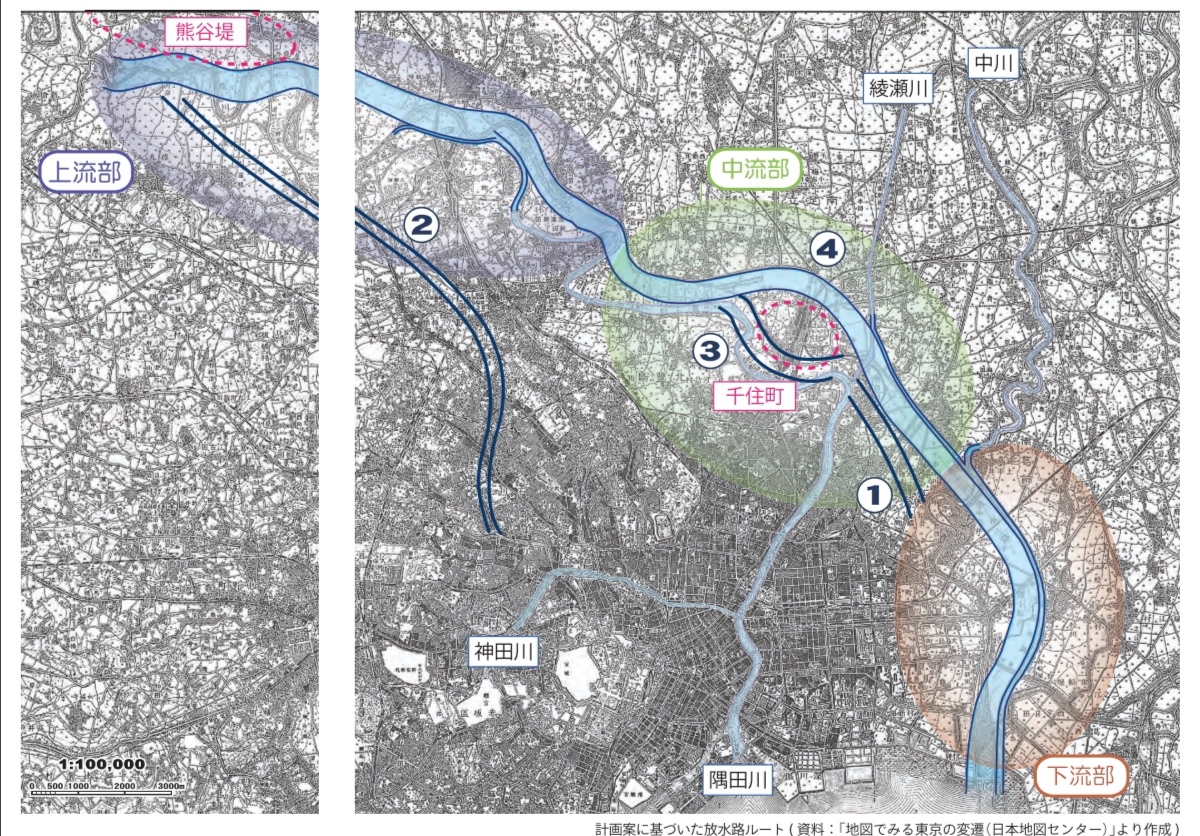
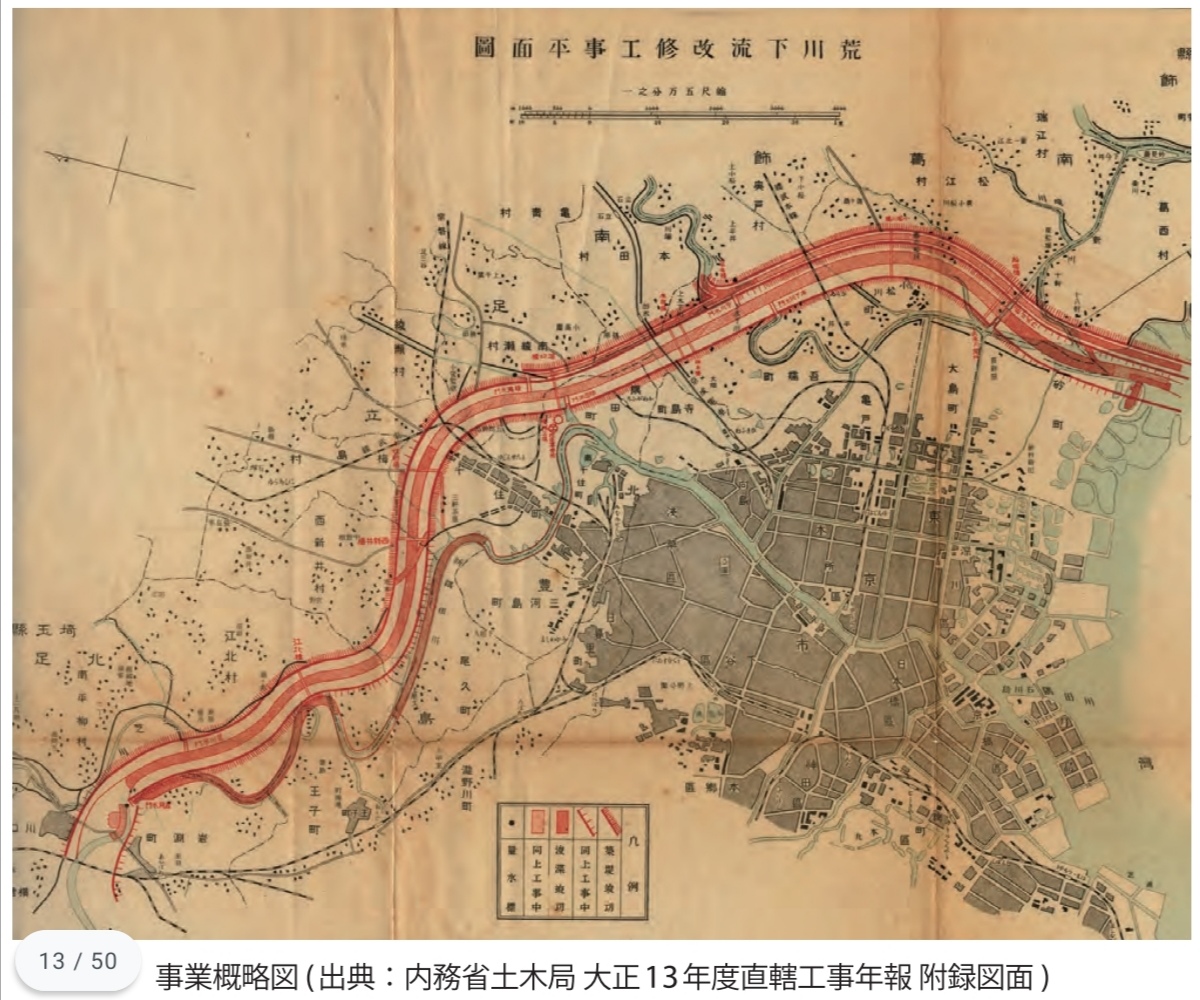
隅田川は基本そのままに、どでかい荒川放水路を作った
その別れ道に一工夫必要
荒川放水路は大きな台風に耐えられるように作ったけど
隅田川は以前のまま
耐えられる水量は桁が違う
よし、入口に水門を作って、台風の時は、隅田川に水が流れ込まないようにしよう
あったま良いー
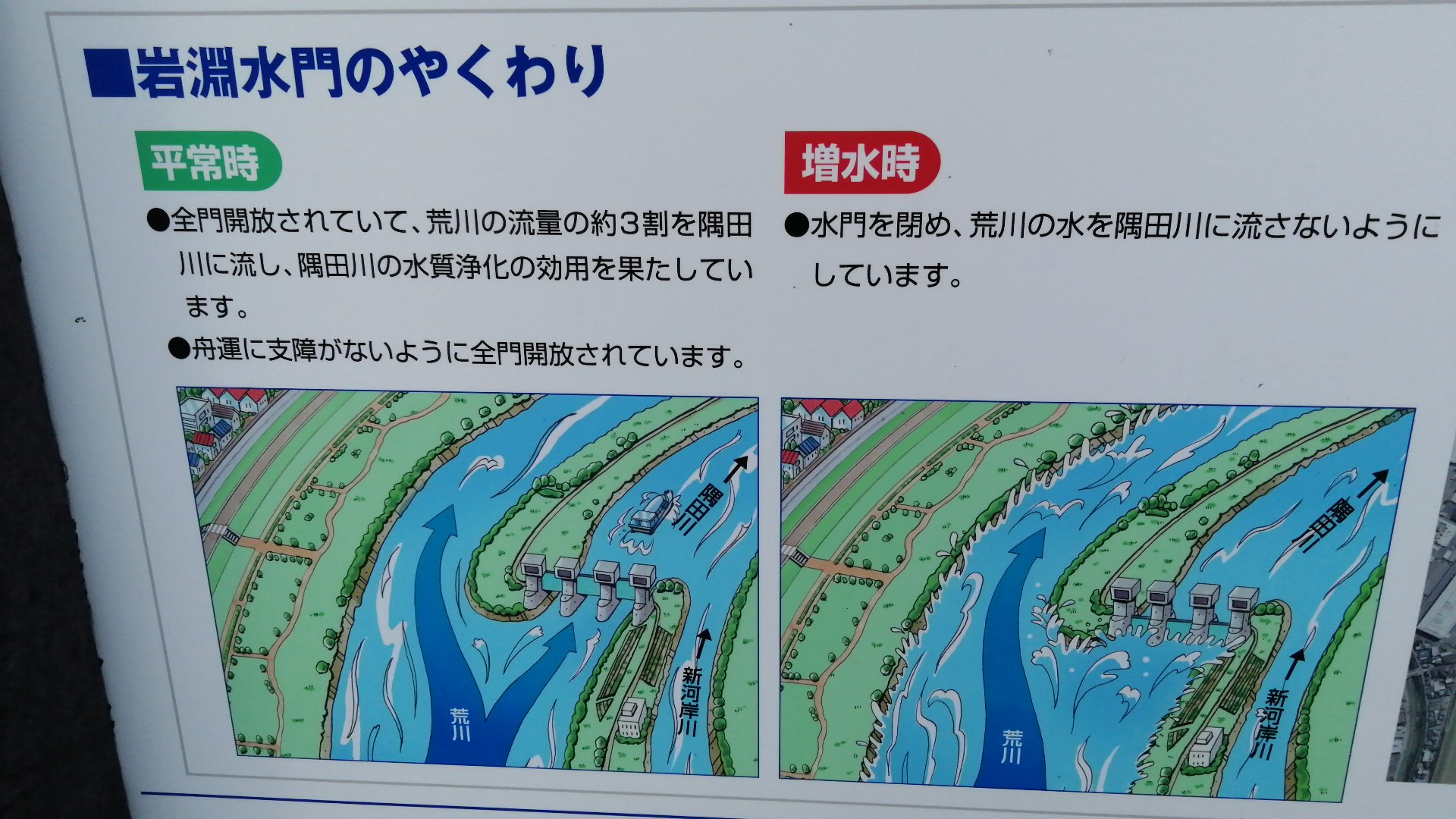
ってところまでは思い付いたけど、それまでに日本にある水門と規模が違いすぎて、どうしていいものやら
水門、水門
パナマ運河の水門を真似れば良いんじゃない
いたー
日本人で唯一、パナマ運河の工事に携わり、最終的には現地で副技師長になっちゃったすごい人
お願いしまーす
青山士(あきら)

大学を出てまもなく、恩師の勧め
パナマ運河の工事が行われるらしいよ、行ってみたら?
面白そうですね。行ってきまーす
行ってみると、7年半で4000人が亡くなるほどの過酷な環境
青山もマラリアに感染し、生死の淵をさまよいます
当時を振り返ってこう語っています
「天然との戦争で大いなる苦痛を伴うものでありますが、今になって顧みると血湧返るを覚えて愉快のこともあります」
岩淵水門の工事を任された青山
パナマ運河で、特に基礎工事の大切さを痛感
岩淵水門の基礎は、川底よりさらに20mの深さに
鉄筋コンクリートの枠を6個埋めて固めてあります。
当時「そこまで頑丈にする必要があるのか」という声もありました
青山は譲りませんでした。
結果的に、大正12年(1923)の関東大震災にも被害を受けず完成に至りました。
でしょ。そうなんですって

カスリーン台風
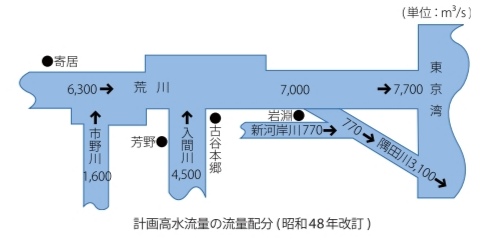
荒川放水路完成後の昭和初期、
荒川では10年間に3度も計画高水流量を上回る大きな洪水が発生しました。
そのうち、昭和22年(1947)のカスリーン台風は、
荒川のみならず東日本全域に大きな爪あとを残しました。
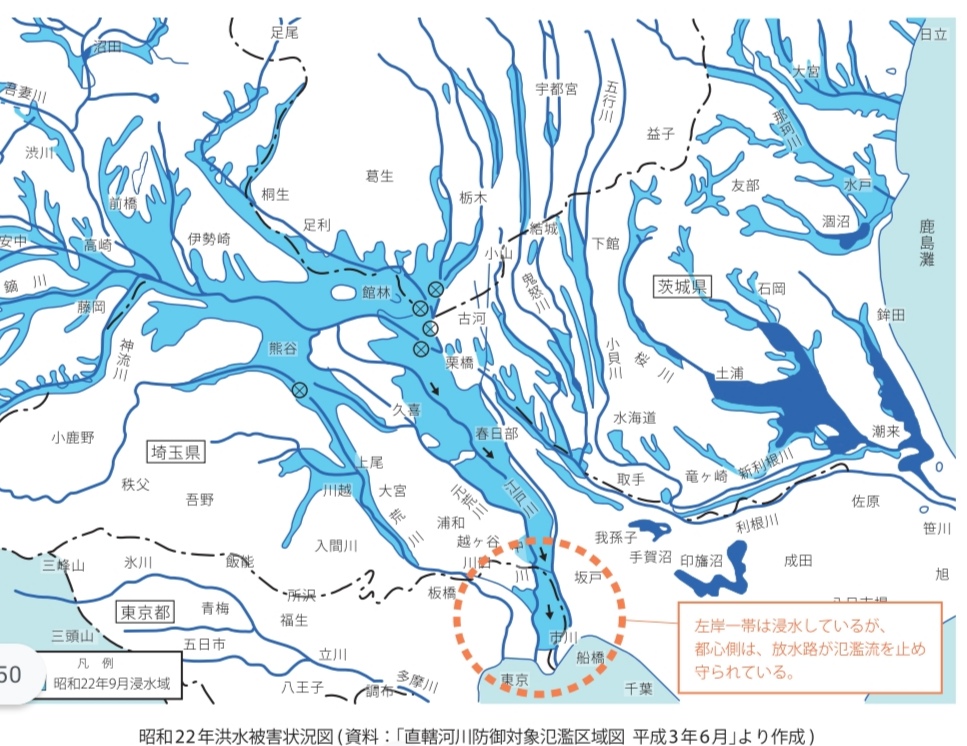
それでも洪水になったのは、荒川上流。
荒川放水路部分は堤防の決壊なし
岩淵水門がガッチリ塞いで隅田川を守り
隅田川も氾濫なし
結果は良かったものの、10年間に3度も計画高水流量を上回るとなるとヒヤヒヤもの
岩淵水門も強化せねば
昭和35年に大規模改修工事
さらに、昭和48年荒川基本計画が改訂
水門にもう少し高さが必要ってことになった
作り替えるぞ
青山士の作った岩淵水門は旧岩淵水門、通称赤門となり
歴史的建造物なのでオブジェとして残り
どでかい青門が誕生しました

位置関係的には
まず、赤門だけのとき

こうなって

こう

今、こんな感じ
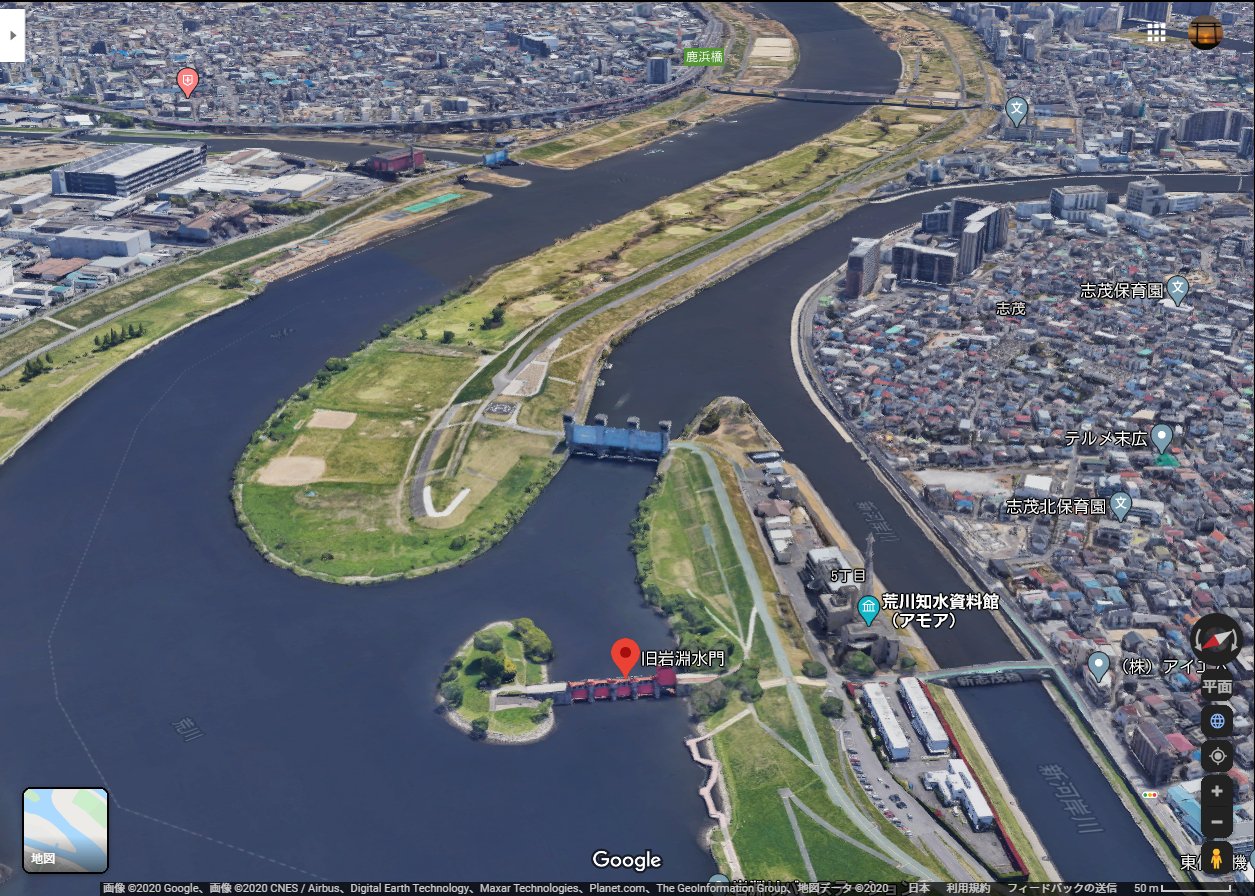
実際にどう役立ったかというと
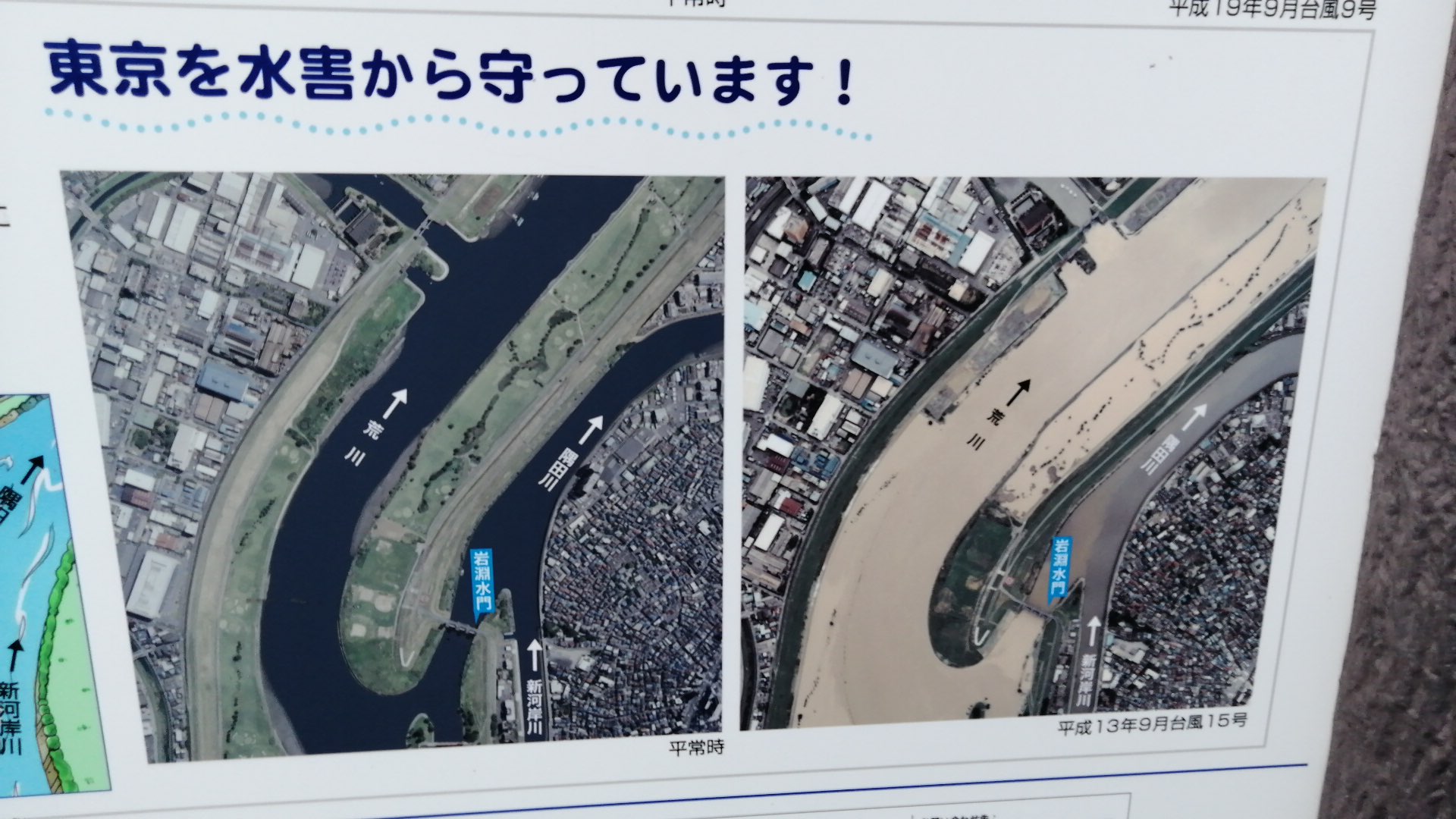
平成13年の台風の時
まっ茶色の泥水が、河川敷全てを埋め尽くしているなか、隅田川手前でガッチリガード
隅田川は泥水が入っていません
東京都心が守られたのです
記憶に新しい2019年(令和元年)
多摩川が氾濫したあの台風19号でも頑張ってくれたのです
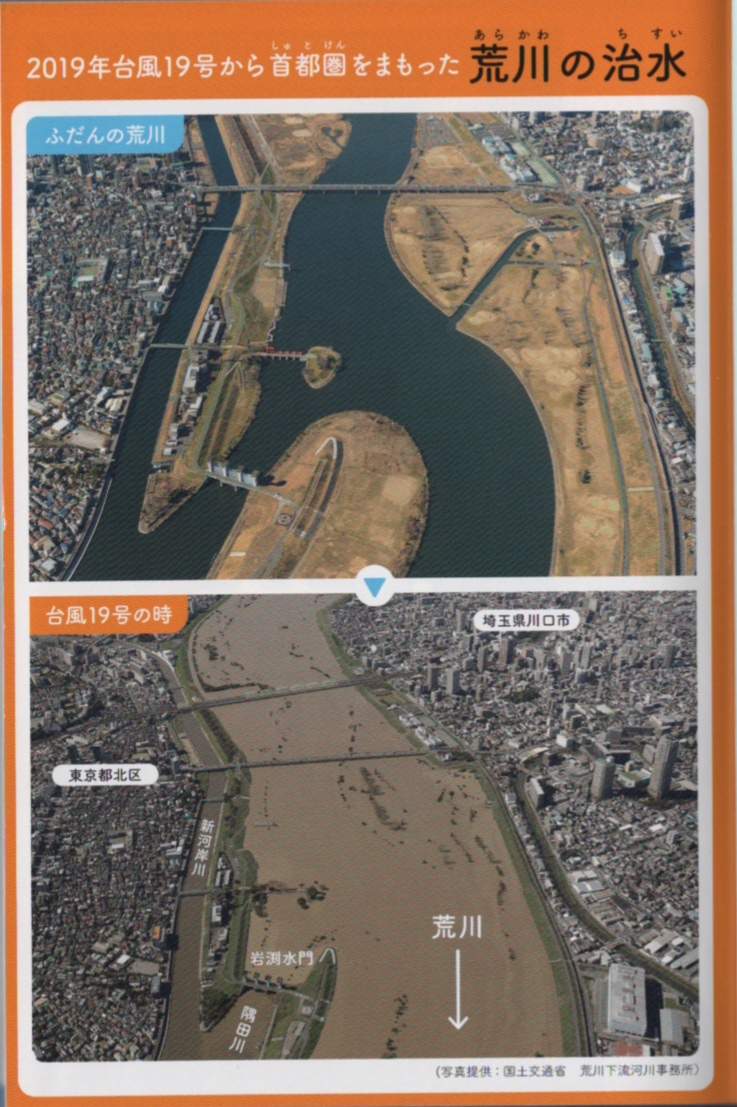


後に調べて分かったのは、荒川の水位は隅田川の堤防の高さを27cm上回っていた
即ち、岩淵水門を閉めていなければ、隅田川は氾濫していた
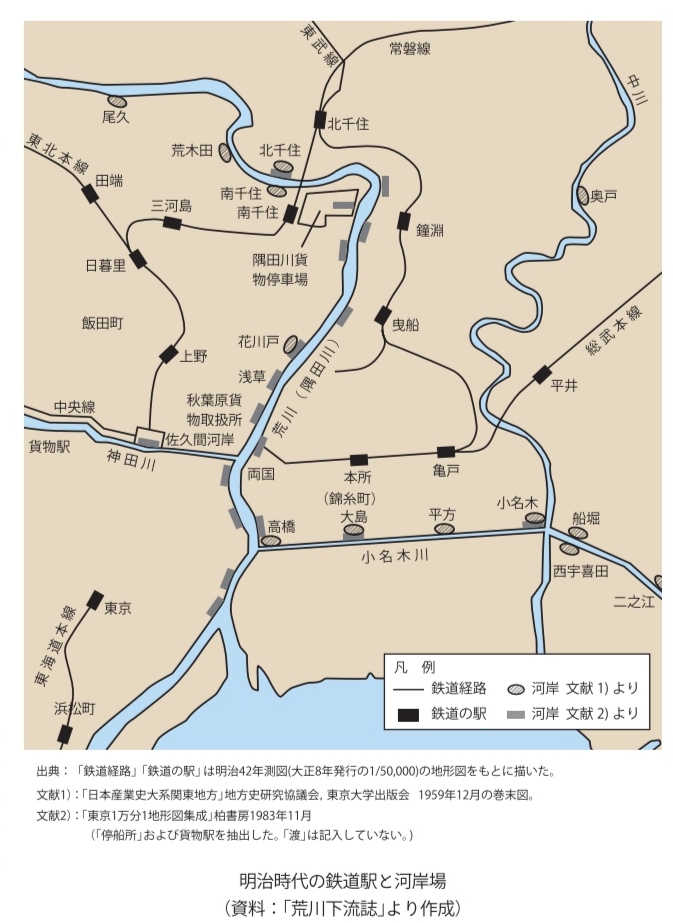
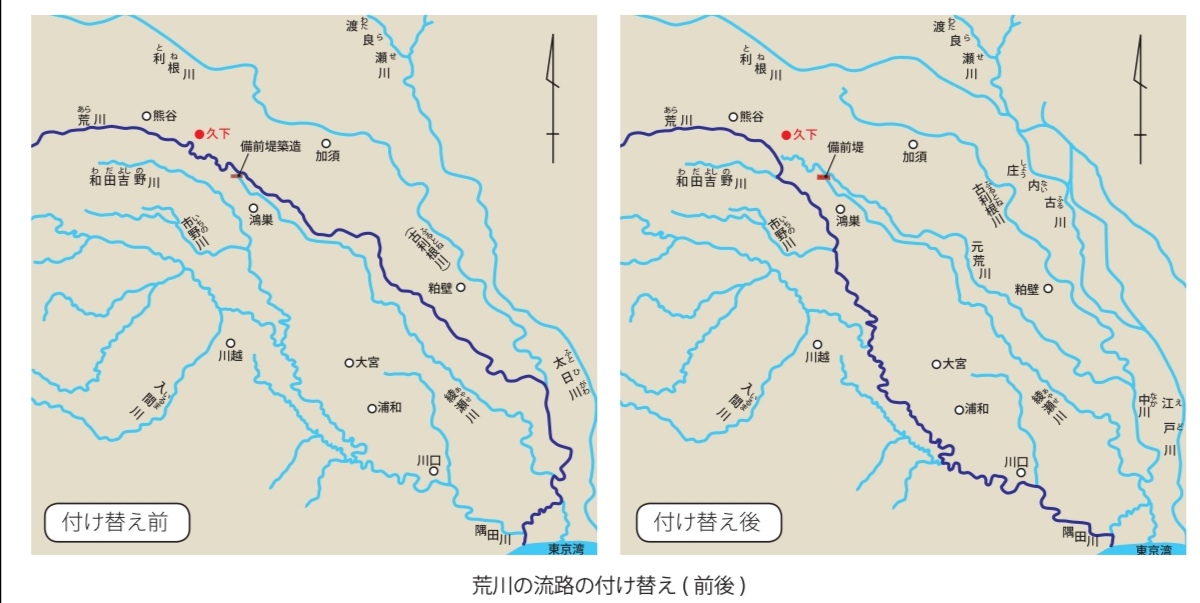 舟運と治水では水の量だけでなく、川の曲がり具合の都合も逆になる
舟運と治水では水の量だけでなく、川の曲がり具合の都合も逆になる